- JC.kim

- 2018년 9월 14일
- 5분 분량

오늘은 JMP를 이용해 업종별 매출액과 종업원 수, 자산 등이 나와 있는 예제 파일로 데이터 분석을 실시해보자. (예제 파일은 이메일로 요청하시면 보내드립니다.)

먼저 데이터테이블은 아래 사진과 같이 6개의 Columns와 31개의 Rows로 구성되어 있다. 변수는 각각 업종, 회사명, 매출액, 이익, 종업원 수, 자산 이렇게 나와 있다. 데이터 테이블이 어떻게 구성되어 있는지 한눈에 보려면, [Cols]-[Columns Viewer]을 눌러 확인할 수 있다.

그럼 이 데이터의 분포를 확인해 보자. 통계분석의 기본은 데이터가 어떻게 구성되어 있는지 파악하는게 가장 중요하다. 그리고 JMP의 Distribution 기능을 이용하면, 각 변수마다 대략적인 경향성을 파악할 수 있다.

이제 이 데이터들이 어떻게 분포하며, 어떤 평균값을 갖는지, 어떤 경향을 띄는지 파악 했다. 이제 아래의 가이드 라인을 따라 이 데이터를 활용한 여러 가지 분석을 실시하였다.
1. Formula 기능 활용하여 ‘매출액 대비 이익률’이 가장 높은 상위 회사 파악하기
먼저 새로 데이터 Columns을 만들어, ‘종업원 당 매출액’ 과 ‘매출액 대비 이익률’을 회사마다 계산해 보자. 새로 변수가 만들어질 공간에 마우스 커서를 놓고, 마우스 오른쪽 버튼을 눌러 새로운 Columns을 추가한다. 하나는 ‘종업원 당 매출액’ , 다른 하나는 ‘매출액 대비 이익률’을 만들어 준다.

종업원당 매출액은 매출액을 종업원 수로 나누면 된다. 또, 매출액 대비 이익률 또한 이익을 매출액으로 나누면 된다. 그럼 이를 Formula를 이용하여 해보자.
해당 Columns을 클릭하고, 우 클릭 하면, [Column Properties]-[Formula]를 누른다.
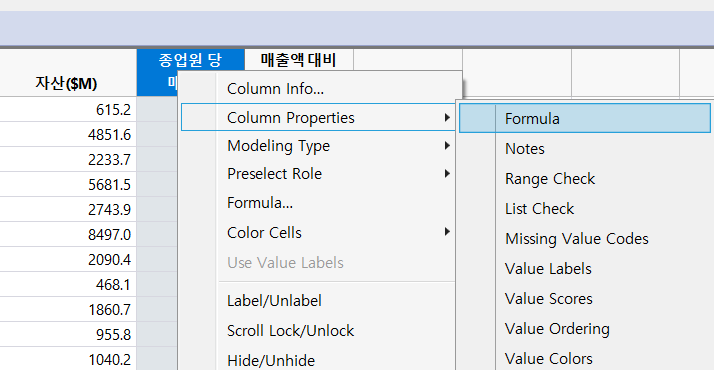
각각의 변수를 위의 얘기한 방식대로 작성 해 준다.

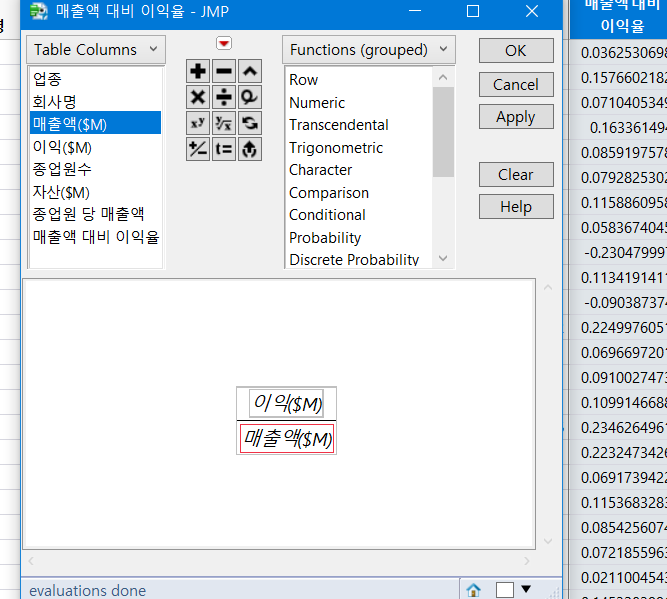
그러면 우리가 원하는 변수의 값들을 위와 같이 계산할 수 있다.
이제, Table의 Sort 기능을 이용해, ‘매출액 대비 이익률’이 높은 상위 회사를 찾아보자.
[Tables]-[Sort] 기능을 누른 뒤, 아래 그림처럼 변수를 선택하고, 숫자가 높은 순서대로 정렬해야 하니까, Descending 버튼을 눌러 (아래 빨간색 부분) ‘OK’를 눌러보자.

그러면 아래와 같이 새로운 데이터 테이블이 형성됨을 볼 수 있으며, ‘매출액 대비 이익률’이 높은 회사부터 순서대로 볼 수 있다.

2. 종업원의 수에 따라 대기업, 중기업, 소기업으로 분류하기
이번에는 Formula 기능을 이용해 ‘종업원 수’에 따라 기업을 분류해 보자. 위와 같이 새로운 테이블을 만들어, Formula에 수식을 아래와 같이 작성하였다. 종업원 수가 40000명 이상의 기업은 ‘대기업’ 20000명 이상, 40000명 이하는 ‘중기업’, 20000명 이하는 ‘소기업’으로 분류하였다.

Conditional 메뉴의 If 문을 이용하여,

이와 같이 수식을 만들어 ‘OK’.
그럼 아래와 같이 ‘기업분류’ 변수가 완성되었음을 볼 수 있다. 여기서 중요한 것은, JMP는 자동으로 DataType을 정해준다는 것이다. 왼쪽에 DataType을 보면, 기업분류 항목이 Nominal로 되었음을 알 수 있다.

3. Tables의 Summary기능을 이용하여, ‘업종’ 및 ‘기업 분류’ 별로 평균치 계산하기
이번엔 Summary 기능을 이용해 기존 테이블에 있는 연속형 자료의 평균을 구해 새로운 데이터 테이블을 만들어 보자. 먼저 업종별로 ‘평균 매출’, ‘평균 종업원 수’, ‘평균 자산’을 구해보자.
[Tables]-[Summary]를 눌러 아래와 같이 입력해 준다. Mean, 평균을 계산하려면, 먼저 변수를 클릭한 뒤, Statistics를 눌러 아래 Mean을 선택하면 된다.

그럼 아래와 같이 새로운 데이터 테이블이 형성 되었음을 보게된다.

같은 방식으로 ‘기업 분류’ 별 평균값들을 계산 해 보자.

4. Skewness, CV, Interquartile Range
이번엔 Distribution 과 Data Filter 기능을 이용해 Skewness, CV, Interquartile Range 값을 알아보자. 먼저 Skewness, CV, Interquartile Range, 이 세 가지 통계량의 의미는 무엇일까?
Skewness (비대칭도)
이는 확률, 통계이론에서 비대칭도, 왜도라고 불리는 값이며, 실수 값, 확률 변수의 분포 비대칭 정도를 나타내는 지표이다. 아주 대칭적인 분포에서는 이 Skewness가 0이 나온다. 그러나 분포가 오른쪽으로 치우치면 양수, 왼쪽으로 치우치면 음수의 값을 나타내게 된다. 표본 왜도에 대한 수학적 수식은 아래와 같다. (위키백과)

CV (Coefficient of Variation, 변동계수)
CV 값은 표준편차를 평균으로 나눈 값이며, ‘상대표준편차(RSD)’라고도 부른다. 이는 측정단위가 서로 다른 자료들을 비교할 때, 사용된다. 이 변동 값이 크면 클수록, 자료들 간 상대적인 차이가 크다는 의미이다.
Interquartile Range (IQR, 사분 범위)
Interquartile Range는 연속형 자료의 분포를 25%,50%,75%로 나눠, 50%를 기준으로 데이터 값이 얼마나 흩어 졌는지 나타내는 범위이다. 이는 Q3-Q1 값을 이용해 구해질 수 있다. 즉 75%인 부분에서 25% 부분을 빼, 50% 기준으로 앞뒤 25%내의 데이터 범위를 구할 때 사용된다.
그럼 JMP를 이용해 이 세가지 값을 확인해보자. 먼저 우리는 Data Filter 기능을 이용해 ‘제약회사’만 추출하여 통계량을 확인해 볼 것이다. [Rows]-[Data Filter]를 눌러서, ‘업종’을 누르고, add를 누른 뒤, ‘제약회사’를 선택한다.


제약회사만 선택된 모습을 볼 수있다. 이 상태에서 [Analyze]-[Distribution]을 누른 뒤, 매출액을 Y.Columns에 넣고 ‘OK’를 누르면 아래와 같이 데이터를 얻을 수 있다. 그래프를 보기 불편하면 왼쪽 상단 RPM(빨간색 삼각형버튼)을 누른뒤, Stack을 눌러준다.
그리고 Skewness, CV, Interquartile Range를 확인하기 위해, Summary Statistics옆 RPM을 키보드의 [Ctrl]키를 누름과 동시에 눌러 [Customize Summary Statistics]를 선택한다.

그럼 아래와 같은 창이 생성되는데, 여기서 우리가 필요한 Skewness, CV, Interquartile Range항목을 체크 해준뒤, ‘OK’버튼을 눌러보자.

그럼 아래와 같이 Skewness, CV, Interquartile Range 값을 얻을 수 있게 되었다.

통계적 결론
Skewness = 1.26
=> ‘제약회사’의 분포는 오른쪽으로 1.26배 정도 치우쳐 져 있다.
CV = 83.33
=> ‘제약회사’의 상대적 표준편차는 크다.
Interquartile Range = 4356.6
=>‘제약회사’의 사분범위는 중앙을 기준으로 앞뒤로, 4356 만큼 퍼져있다.
5. 회귀분석
이번엔 Fit Y by X 기능을 이용해 회귀분석을 해보자. 먼저 우리는 제약회사에서 ‘종업원 수가 많을수록 매출액이 많을 것이다‘라는 가정을 세워 보도록 하자. 여기서 둘 다 연속형 데이터 이므로, 회귀분석을 실시해 과연, 종업원 수가 많을수록 매출액이 많은지 확인 해 볼 것이다. 통계적 가설은 아래와 같이 세웠다.
귀무가설 H0 = 종업원 수와 매출액과의 관계는 상관이 없다.
대립가설 Ha = 종업원 수와 매출액과의 상관관계가 존재한다.
위의 DataFilter가 켜져있는 상태에서, [Analyze]-[Fit Y by X]를 누르고, 아래와 같이 채워준다.

그리고, 맨 위 왼쪽 RPM을 눌러 [Fit Line]을 누르면, 회귀식이 나오게 된다.

여기서의 회귀식은 y = 1059.68 + 0.092x 가 된다.
그럼 위의 구한 회귀 식이 과연 얼마나 맞아 떨어지는지 확인해 보자. 바로 아래 Lack of Fit 메뉴를 확인해 보자. 이 메뉴는 현재 실시한 분석결과가 얼마나 잘 맞는지 (어울리는지) 판단해 준다.

여기 Max RSq 값이 0.9969 가 나왔다. 즉, 이 분석에서 회귀분석이 어울릴 확률이 99.69% 라는 뜻이다. 다시 말하면, ‘이 데이터에 대한 회귀분석은 적절하다’라는 뜻이 된다. 그리고 아래 통계량도 확인해 보자

우리가 아까 가설을 세웠던 것에 P.value값이 나와있다. 첫 번째 항목에 Prob>F 값이 0.001 보다 작다. 즉 유의 수준 5%이내에서 보통가설이 참일 확률을 의미한다. 다시 말하면, ‘귀무가설이 기각되었다’라는 뜻이고 이는 우리가 세운 대립가설, ‘종업원 수와 매출액과의 상관관계가 존재한다.’ 이 가설이 참이 된다는 의미이다.
통계적 결론 : 귀무가설기각
사실적 결론 : 종업원 수와 매출액과의 상관관계가 존재한다.
그럼 우리가 위의 회귀 식을 이용하여, 예측을 할 수도 있을까. 아주 간단하다. 우리가 위에서 도출한 식 y = 1059.68 + 0.092x 이곳에 원하는 값을 넣으면 특정 결과를 예측해 낼 수 있다. 가령 종업원(x변수)이 7000명인 경우 매출액은 얼마로 예상 되겠는가? y = 1059.68 + 0.092x 이 식 x 에 7000을 넣으면, 1703.68 이라는 값이 나오게 된다.
(매출액) = 1059.68 + 0.092*(종업원수)
6. T-test
이번에는 두 집단 간 유의차가 존재한지 분석해 보자. 업종별 매출액 대비 이익률이 얼마나 차이 나는지 확인해 보기 위해 T-test를 사용해 볼 수있다. T test는 모집단에 대한 정보가 부족할 때, 표본의 수가 적을 때 주로 사용된다. 통계적 가설은 아래와 같이 세울 수 있으며, Fit Y by X 기능을 이용해 쉽게 결론을 낼 수 있다.
귀무가설 H0 = 제약회사와 컴퓨터 회사의 매출대비 이익률의 차이는 없다.
대립가설 Ha = 제약회사와 컴퓨터 회사의 매출대비 이익률의 차이가 존재한다.
[Analyze]-[Fit Y by X]를 눌러, X에 ‘업종’, Y에 ‘매출대비 이익률’을 넣고 ‘OK’. 그리고 왼쪽 위 RPM을 눌러 [t test]를 선택하면 아래와 같은 결과가 나온다.

우리는 가설을 ‘양측검정’ 즉, 두 집단의 차이가 존재하는지 확인하려 했기 때문에, 위의 결과에서 Prob >|t| 의 P.value를 확인하면 된다. P값이 5%보다 작으므로,
통계적 결론 : 귀무가설 기각
사실적 결론 : 제약회사와 컴퓨터 회사의 매출대비 이익률의 차이가 존재한다.
만약 우리가 대립 가설을, ‘제약회사보다 컴퓨터 회사의 매출대비 이익률이 낮을 것이다’라고 잡았다면, 어떻게 될까? 이때는 양측검정이 아닌 단측검정(좌측검정)을 실시해야 하며, 양옆으로 2.5%의 범위가 아닌 왼쪽으로 5% 범위를 확인하게된다. 위의 Prob >t 값이 5% 이상이므로, 단측 검정에서는 귀무가설기각실패, 즉 ‘제약회사보다 컴퓨터회사의 매출대비 이익률은 낮지 않다‘라는 결론을 얻을 수 있을 것이다.
결론적으로 위의 통계치를 사실적 결론으로 적으면 아래와 같다.
- 제약회사와 컴퓨터 회사의 매출대비 이익률의 차이가 존재한다.
- 컴퓨터회사보다 제약회사가 매출대비 이익률이 높다.
- 제약회사보다 컴퓨터회사의 매출대비 이익률은 낮지 않다.
이 세 가지 결론이 한번에 나올 수 있다는 것에 동의하는가? 즉 유의수준의 범위, 신뢰구간을 어떻게 정하고 어떤 분석을 하느냐에 따라 통계적 결론이 달라지며, 통계적 결론이 달라지므로 사실적 결론 또한 달라지게 된다.
7. Bubble Plot
마지막으로 Bubble Plot을 이용하여, 여러 가지 변수들간의 관계를 한눈에 보도록 하자.
[Graph]-[Bubble Plot]을 누르고, 아래처럼 채워 넣는다.

그럼 아래와 같은 결과를 확인할 수 있다.

오늘은 기업데이터를 이용해, 여러가지 통계분석을 실시해 보았다. JMP에 관련한 데이터 분석교육은 이노벨류파트너즈 컨설팅 기업이 전담해서 진행중이다. 빠른 통계분석과, 복잡한 코딩없이 문제를 파악하고 모델링하기에 최적화 되어있다. 매주 토요일마다 JMP를 활용한 빅데이터 분석 교육이 진행 되니, 아래의 홈페이지를 들어가 꼭 교육을 듣기를 추천한다.
대학생인 경우 저렴한 가격으로 교육을 받을 수 있으며, 현재 8월 과정도 단국대에서 진행중이다.



























